Why two parties can't represent you, and what information theory says about it
January 3, 2026
We often talk about politics in terms of ideology, history, or tribalism. But at its core, governance is a compression problem: how do you aggregate the distinct preferences of millions of people into a single output — policy?
In this post, I restrict attention to the simplest possible setting — every policy issue is binary (Yes or No) — and show that even here, the mismatch between voter preferences and party systems is not a bug but a mathematical inevitability. The argument rests on a clean information-theoretic observation: a $k$-party system is a channel with $\log_2 k$ bits of capacity, and when the entropy of voter preferences exceeds that capacity, information is irreversibly lost.
The real world is far messier than binary issues, so the problems identified here are a lower bound on the true difficulty.
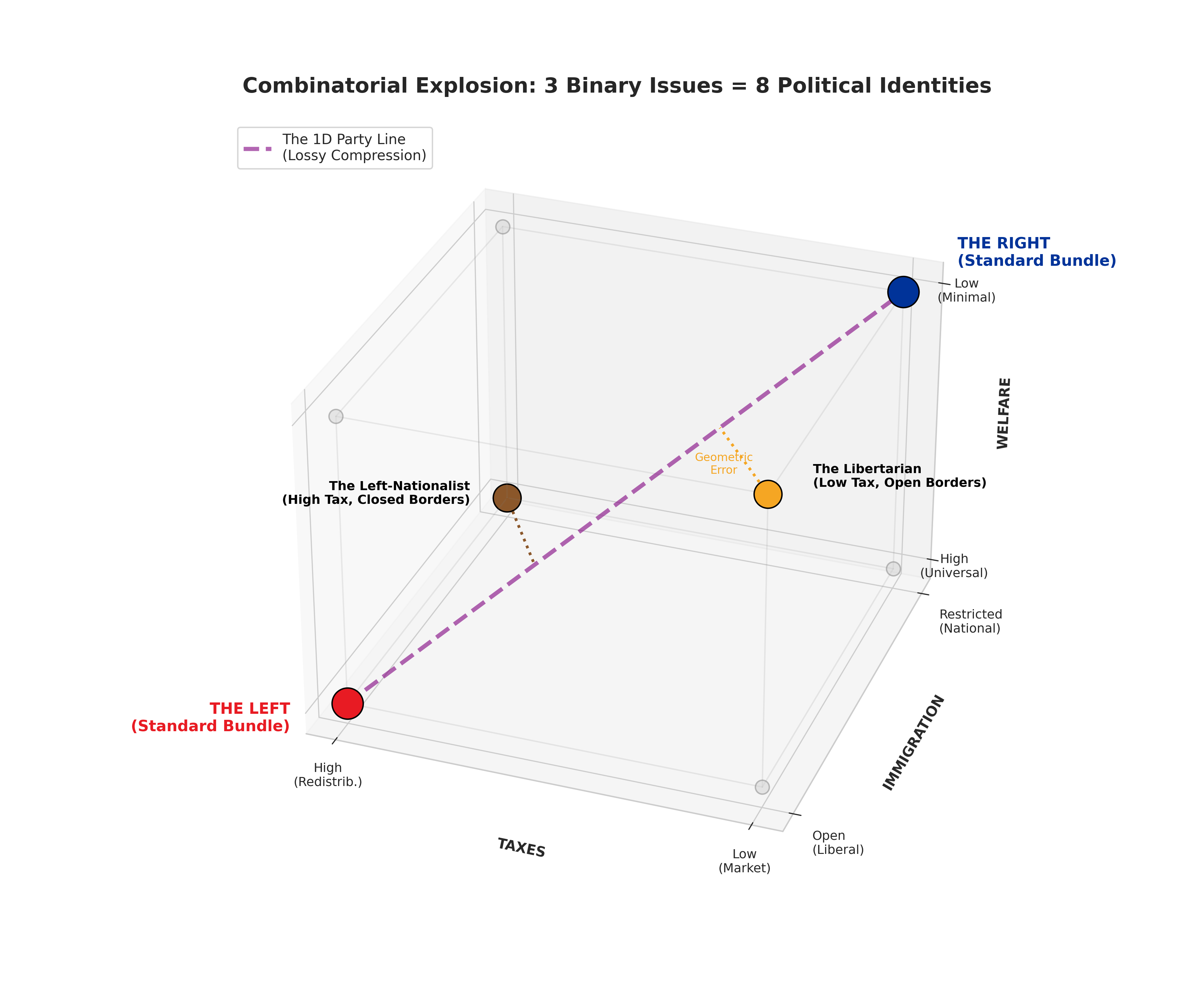
Figure 1: Three binary issues define a cube with $2^3 = 8$ corners — eight distinct political identities. A two-party system compresses this cube onto a single diagonal line (the “party line”), leaving 6 of the 8 positions unrepresented. Voters at those orphaned corners must choose the lesser of two evils.
1. Setup: Preferences as Binary Vectors
Suppose there are $n$ binary policy issues. For concreteness, take $n = 3$:
- Progressive Wealth Tax? (Y/N)
- Nuclear Power Expansion? (Y/N)
- Universal Basic Income? (Y/N)
Each voter’s preference is a binary vector $v \in {0, 1}^n$. With $n = 3$ issues, there are $2^n = 8$ possible preference profiles — the corners of a hypercube.
A society is a probability distribution $p$ over ${0, 1}^n$: the fraction of voters holding each preference profile.
The entropy of the electorate is:
\[H(p) = -\sum_{v \in \{0,1\}^n} p(v) \log_2 p(v)\]This measures how much “political diversity” exists. At one extreme, if everyone agrees ($p$ is concentrated on a single corner), $H(p) = 0$. At the other extreme, if preferences are uniformly distributed, $H(p) = n$ bits.
2. Parties as Codebooks: The Vector Quantisation View
A $k$-party system offers voters a menu of $k$ platforms $\{c_1, \ldots, c_k\} \subset {0,1}^n$. Each voter is assigned to the nearest party (the one matching on the most issues). This is exactly vector quantisation (VQ): we are compressing $2^n$ possible preference vectors into $k$ codewords.
The distortion of this compression is the expected Hamming distance between a voter’s true preference and their assigned party:
\[D = \sum_{v} p(v) \min_{j} d_H(v, c_j)\]where $d_H$ is the Hamming distance — the number of issues on which the voter and their party disagree.
A voter with distortion $d$ is being misrepresented on $d$ issues. This is the formal version of “the lesser of two evils.”
3. The Two-Party System as a 1-Bit Channel
In a two-party system ($k = 2$), the voter’s ballot carries exactly 1 bit of information: Party A or Party B.
But the space of preferences has $2^n$ elements, requiring up to $n$ bits to specify. The act of voting compresses an $n$-bit preference vector into a 1-bit message. By the source coding theorem, this compression is only lossless when the entropy of the source is at most 1 bit.
This gives us a precise criterion:
A two-party system is adequate if and only if $H(p) \leq 1$ bit.
When it works: Low-entropy electorates
Suppose 50% of voters hold preference $(0,0,0)$ (“The Left”) and 50% hold $(1,1,1)$ (“The Right”). Then:
\[H(p) = -2 \times 0.5 \log_2 0.5 = 1 \text{ bit}\]A two-party system with $c_A = (0,0,0)$ and $c_B = (1,1,1)$ achieves zero distortion — every voter is perfectly represented. The 1-bit channel suffices because the electorate only uses 1 bit of the available $n$-bit space.
This is the scenario that two-party advocates implicitly assume: that political preferences are highly correlated, clustering neatly into “Left” and “Right” bundles.
When it fails: High-entropy electorates
Now suppose voters are uniformly distributed across all 8 corners. Then $H(p) = 3$ bits, but the channel capacity is still 1 bit. No matter how cleverly we choose $c_A$ and $c_B$, we must lose at least $3 - 1 = 2$ bits of information.
Concretely, with $c_A = (0,0,0)$ and $c_B = (1,1,1)$, consider the voter at $(1,0,1)$ — a “Libertarian” who wants low taxes and minimal welfare but open immigration. Their nearest party is $c_B = (1,1,1)$, at Hamming distance 1. But a voter at $(0,1,0)$ — a “Left-Nationalist” who wants high taxes and strong welfare but closed borders — is nearest to $c_A = (0,0,0)$, also at distance 1. Both are misrepresented on one issue.
The expected distortion for the uniform distribution with optimal two-party placement is:
\[D = \frac{1}{8}\sum_{v \in \{0,1\}^3} \min(d_H(v, c_A), d_H(v, c_B))\]With $c_A = (0,0,0)$ and $c_B = (1,1,1)$, the distances are:
| Voter $v$ | $d_H(v, c_A)$ | $d_H(v, c_B)$ | $\min$ |
|---|---|---|---|
| $(0,0,0)$ | 0 | 3 | 0 |
| $(0,0,1)$ | 1 | 2 | 1 |
| $(0,1,0)$ | 1 | 2 | 1 |
| $(1,0,0)$ | 1 | 2 | 1 |
| $(0,1,1)$ | 2 | 1 | 1 |
| $(1,0,1)$ | 2 | 1 | 1 |
| $(1,1,0)$ | 2 | 1 | 1 |
| $(1,1,1)$ | 3 | 0 | 0 |
On average, each voter is misrepresented on 0.75 out of 3 issues — 25% of their preferences are lost. And 6 out of 8 voter types (75%) are imperfectly represented.
4. The General Rate–Distortion Tradeoff
More generally, a $k$-party system provides $R = \log_2 k$ bits of representation. The relationship between rate and distortion is governed by rate–distortion theory.
For a uniform source over ${0,1}^n$ with Hamming distortion, the rate–distortion function is:
\[R(D) = n - H_b\!\left(\frac{D}{n}\right) \cdot n\]where $H_b(p) = -p\log_2 p - (1-p)\log_2(1-p)$ is the binary entropy function. To achieve distortion $D$, you need at least $R(D)$ bits — i.e., at least $2^{R(D)}$ parties.
This formalises the tradeoff:
| Parties ($k$) | Bits ($R$) | Min. distortion (uniform, $n=3$) |
|---|---|---|
| 2 | 1 | 0.75 |
| 4 | 2 | ~0.375 |
| 8 | 3 | 0 |
To achieve zero distortion with $n$ binary issues, you need $k = 2^n$ parties — one for every corner of the hypercube.
5. The Curse of Dimensionality
The table above reveals the fundamental problem: the number of parties required for lossless representation grows exponentially in the number of issues.
For $n = 3$, we need 8 parties — manageable. But for $n = 10$ issues, we need $2^{10} = 1{,}024$ parties. For $n = 30$:
\[2^{30} \approx 1 \text{ billion parties}\]This is the curse of dimensionality applied to governance. No ballot can present a billion options. The cognitive and institutional costs make this impossible.
This creates an inescapable dilemma:
- Few parties ($k = 2$): Low cognitive cost, but high distortion — voters are systematically misrepresented.
- Many parties ($k \to 2^n$): Low distortion, but impossible cognitive and institutional overhead.
We cannot “party” our way out of this problem.
When does the curse bite?
The severity depends on the entropy of the electorate. If voter preferences are highly correlated (low entropy), most of the $2^n$ corners are empty and a small number of parties suffices. The curse bites when preferences are independent across issues — when knowing a voter’s position on taxes tells you nothing about their position on immigration.
In the extreme “impartial culture” model (uniform distribution), the entropy is maximal at $n$ bits, and the full exponential cost is unavoidable. Real electorates lie somewhere between these extremes, but any degree of independence across issues pushes the required number of parties above what is practical.
Critically, the causal direction matters. If voters’ preferences appear correlated because the party system only offers correlated bundles, then the observed low entropy is an artifact of the compression, not a property of the underlying preferences. The system may be manufacturing the conformity it relies on.
6. The Solution: Unbundling Issues
The exponential blowup arises because parties bundle issues — they force voters to buy the whole menu. The solution is to unbundle: let voters express preferences issue by issue.
If each of the $n$ issues is voted on independently, the voter transmits $n$ bits of information — one per issue. This matches the dimensionality of the preference space exactly, achieving zero distortion regardless of the distribution $p$.
Formally, instead of solving one vector quantisation problem in ${0,1}^n$ (requiring $2^n$ codewords for lossless compression), we solve $n$ independent scalar quantisation problems in ${0,1}$ (each requiring just 2 “codewords”: Yes and No). The total cost is $2n$ options instead of $2^n$ — linear instead of exponential.
This is the core idea behind Liquid Democracy and issue-by-issue direct voting:
- Direct vote: On issues you care about, vote directly — transmitting your preference bit with full fidelity.
- Delegation: On issues where you lack expertise, delegate your vote to a trusted representative — effectively choosing a better “codebook” for that single dimension.
The information-theoretic advantage is clear: delegation is per-issue, so the voter’s total representation is a composite of different experts across dimensions, rather than a single lossy codeword that bundles everything together.
Summary
| Two-Party System | Multi-Party System | Issue-by-Issue Voting | |
|---|---|---|---|
| Channel capacity | 1 bit | $\log_2 k$ bits | $n$ bits |
| Distortion (uniform) | $\frac{n-1}{2n} \cdot n$ | Decreasing in $k$ | 0 |
| Scales with issues? | No | Exponential cost | Linear cost |
| Assumption for adequacy | $H(p) \leq 1$ | $H(p) \leq \log_2 k$ | None |
The mathematics is simple: preferences over $n$ binary issues live in an $n$-dimensional space. Any system that compresses this into fewer dimensions loses information. A two-party system is a 1-bit channel — adequate only when the electorate has at most 1 bit of entropy. As voters become more independent in their thinking, the distortion grows, and the only way to eliminate it is to match the channel capacity to the dimensionality of the preference space.
We don’t need better parties. We need a mechanism that transcends bundling.
References
- Thorburn et al. (2023). Error in the Euclidean Preference Model. arxiv.org/abs/2208.08160