act65

How does Enigma work? Let’s start with the basics.

Caesar Cipher

A Caesar cipher is one of the simplest and most widely known encryption techniques. It’s a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down or up the alphabet. For example, with a shift of 2, ‘a’ becomes ‘c’, ‘b’ becomes ‘d’, …, and ‘z’ becomes ‘b’.

This cipher can be mathematically described using modular arithmetic. If we map letters a-z to numbers 0-25, the encryption of a letter $x$ with a shift $k$ is $E(x) = (x + k) \pmod{26}$. This is also known as a cyclic group.

Substitution Cipher

A substitution cipher is a method of encrypting in which units of plaintext are replaced with ciphertext, according to a fixed system. In a simple monoalphabetic substitution cipher, each letter of the alphabet is mapped to a unique different letter. The “key” is this permutation of the alphabet. This is also known as a symmetry group.

A Stepping Substitution Cipher (Polyalphabetic Idea)

To make ciphers stronger, we can change the substitution key as we encrypt. This is a basic idea behind polyalphabetic ciphers.

In this example, we start with an initial substitution key. After you encrypt a piece of text by pressing the “Encrypt and Step Key” button, the substitution key itself will be modified (shifted by one position, like a Caesar cipher with shift 1). The next time you encrypt text, it will use this new, stepped key.

Mapping Letters to Numbers for Ciphers

Many ciphers, especially more complex ones implemented mathematically or in computers, operate on numbers rather than directly on letters. To use such ciphers for text, we first need a consistent way to convert letters into numbers and then back again.

A common mapping for the English alphabet is:

• ‘a’ = 0
• ‘b’ = 1
• ‘c’ = 2
• …
• ‘z’ = 25

The total number of unique characters in our alphabet (26 in this case) is often denoted by n. So, for English letters, n=26. After encryption, the resulting numbers can be converted back to letters using the same mapping.

EasyEnigma: A Simplified Rotor Cipher

Our EasyEnigma, implemented in Rust, is a simplified model designed to illustrate its core operational principles. While simpler, it captures the essence of how rotors, a reflector, and stepping mechanisms work together to encrypt messages.

EasyEnigma operates as follows:

1. Numerical Alphabet (n): The cipher operates on numbers, typically from 0 to n-1. The variable n in the EasyEnigma struct represents this alphabet size. For example, if we’re encrypting English letters, we might map ‘a’ to 0, ‘b’ to 1, …, ‘z’ to 25, making n=26.

2. Rotors (rotor_wirings, rotor_inv_wirings): The machine features a configurable number of rotors. The wiring for each rotor is a permutation of the n possible inputs. This means each number from 0 to n-1 is mapped to a unique number within the same range for that rotor.
   • In the EasyEnigma struct, rotor_wirings: Vec<Vec<u32>> stores these permutations, one Vec<u32> for each rotor.
   • These permutations are initially created by the generate_permutation(n, rng) function for each rotor when a new EasyEnigma instance is made.
   • For the signal to travel backward through the rotors during encryption, the machine also stores their inverse permutations: rotor_inv_wirings: Vec<Vec<u32>>. These are calculated by the invert_permutation(perm: &[u32]) function for each rotor’s wiring.
3. Reflector (reflector_wiring): A single reflector is used after the signal has passed forward through the rotors. The reflector is also a permutation but has a special property: it’s an involution. This means if it maps a number i to j, it must also map j back to i. A crucial feature of historical Enigma reflectors (and aimed for in generate_reflector for even n) is that no character maps to itself (no fixed points).
   • The reflector_wiring: Vec<u32> in the struct holds this configuration.
   • It’s generated by the generate_reflector(n, rng) function, which attempts to create random pairings.
4. Stepping Mechanism (step): To ensure that the same input character doesn’t always encrypt to the same output character (a key feature of polyalphabetic ciphers), the rotors “step” or rotate. This changes the effective wiring for each character encrypted.
   • EasyEnigma uses a list of counters, step: Vec<u32>, stored in the struct, representing the current rotational offset of each rotor. These are typically initialized to 0 for each rotor.
   • The stepping logic is found at the end of the call_char method. The first rotor (index 0) steps after every character. If it completes a full revolution (its step counter returns to 0), the next rotor (index 1) steps once. If that rotor also completes a revolution, the subsequent rotor steps, and so on, like an odometer:

     // Step for the next character
     if self.step.is_empty() { /* Or handle as an error if no rotors */ return; }
     
     self.step = (self.step + 1) % self.n; // First rotor always steps
     for i in 0..(self.step.len() - 1) {
         if self.step[i] == 0 { // If rotor 'i' completed a full revolution (just turned over to 0)
             self.step[i+1] = (self.step[i+1] + 1) % self.n; // Then rotor 'i+1' steps
         } else {
             // If rotor 'i' did not turn over, then subsequent rotors do not step from this cascade
             break;
         }
     }
     

     This is a simpler “odometer” style stepping compared to the historical Enigma.

5. Encryption Path (within call_char method): When a single number x (representing a character) is encrypted using the call_char(&mut self, x: u32) -> u32 method, it undergoes the following transformations:

   • Forward Pass through Rotors: The input x passes sequentially through each rotor, from the first (index 0) to the last. The transformation through each rotor is handled by the pass_rotor helper function.

     // Forward path
     let mut current_val = x;
     for i in 0..self.rotor_wirings.len() { // Iterate through each rotor
         current_val = Self::pass_rotor(current_val, i, self.step[i], true, self.n, &self.rotor_wirings, &self.rotor_inv_wirings);
     }
     

     The pass_rotor function (fn pass_rotor(val: u32, rotor_idx: usize, step_val: u32, forward: bool, n: u32, wirings: &[Vec<Vec<u32>>], inv_wirings: &[Vec<Vec<u32>>]) -> u32) works like this:

     1. effective_input = (val + step_val) % n;: The input value is shifted by the rotor’s current step position. This simulates the rotation of the rotor relative to a fixed entry point.
     2. If forward is true, wired_output = wirings[rotor_idx][effective_input as usize]; otherwise (for backward pass), wired_output = inv_wirings[rotor_idx][effective_input as usize];. The shifted value then passes through the rotor’s actual fixed wiring (or its inverse).
     3. output = (wired_output + n - step_val) % n;: The result is then shifted back by the rotor’s step value. The + n ensures the modulo arithmetic handles potential negative results correctly.
   • Reflector: The output from the last rotor then enters the reflector_wiring.

     // Reflector
     current_val = self.reflector_wiring[current_val as usize];
     

   • Backward Pass through Rotors: The reflected value then travels back through the rotors, but in reverse order (from the last rotor back to the first) and using their inverse wirings. The pass_rotor function is used again, but with forward set to false.

     // Backward path
     for i in (0..self.rotor_wirings.len()).rev() { // Iterate through rotors in reverse
         current_val = Self::pass_rotor(current_val, i, self.step[i], false, self.n, &self.rotor_wirings, &self.rotor_inv_wirings);
     }
     

     The final current_val after this entire path is the encrypted number.

6. Initialization and Configuration: An EasyEnigma instance is created using the EasyEnigma::new(n: u32, rng: &mut impl Rng) -> Self constructor, which sets up the random rotor wirings (for all configured rotors) and reflector for a given alphabet size n. Users can also define specific configurations using set_wirings(...) or adjust the initial rotor positions using set_steps(...). The reset_steps() method returns the rotors to their 0 position.

My implementation is located here.

EasyEnigma vs. Historical Enigma & Its Differences (More Succinct)

Historical Enigma Briefly: Used 3-5 wired rotors, each performing a full alphabet substitution. Rotors stepped (rotated) in a complex, odometer-like fashion, changing the substitution for each character. A plugboard added an initial/final letter swap, and a reflector ensured self-reciprocity (if A encrypts to B, B encrypts to A, given the same machine state) and that no letter encrypted to itself.

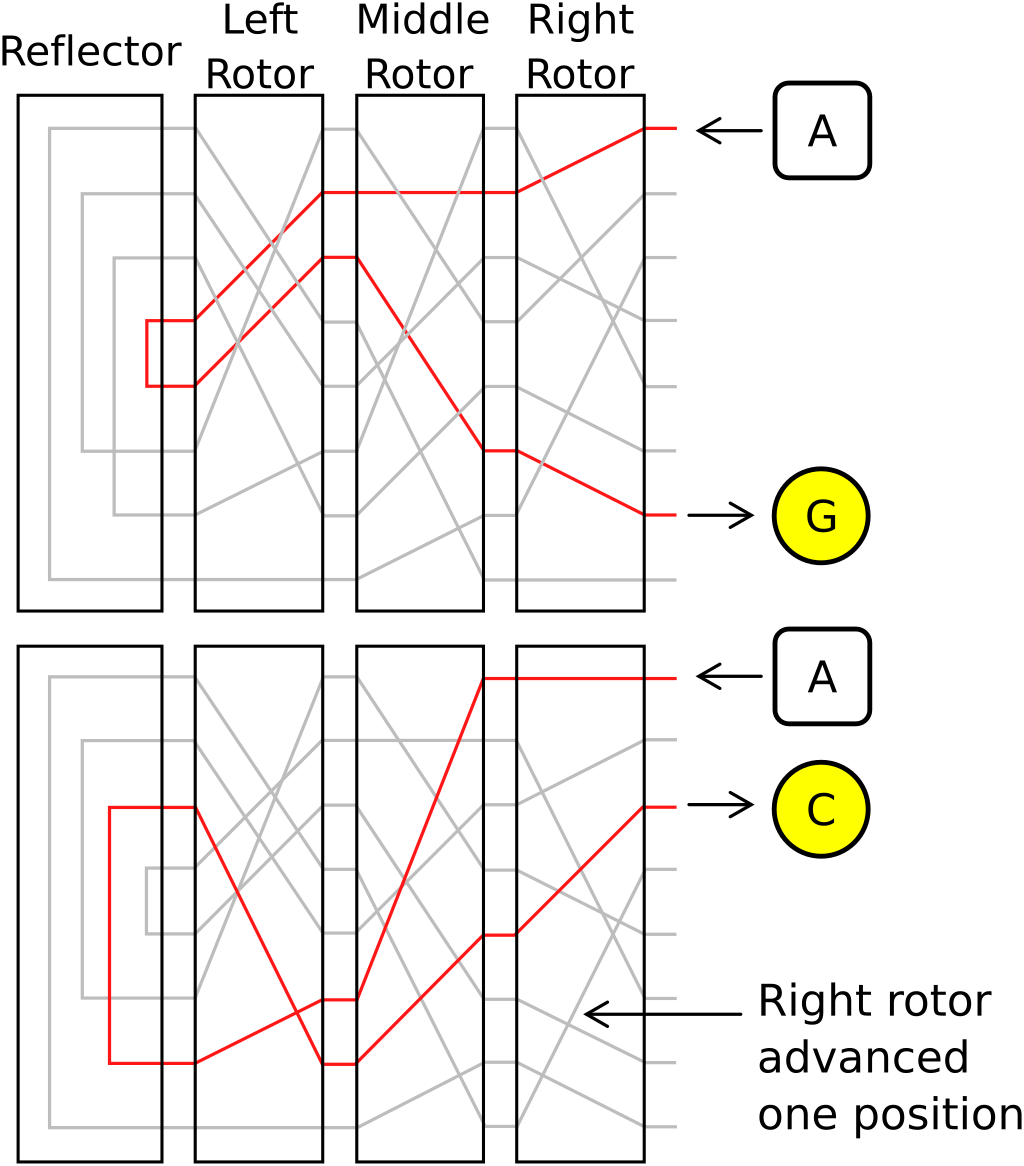
Our EasyEnigma aims to demonstrate the core ideas of a rotor cipher, but there are some differences to the historical Enigma machines used in WWII:

• Core Similarities: Both use rotating substitution units (rotors) that change with each character, a reflector, and a path for the signal through rotors, reflector, and back. This creates a polyalphabetic cipher where the substitution changes constantly.
• Key Differences:
  • Complexity: EasyEnigma supports a configurable number of rotors and uses a simple odometer-style stepping. Historical Enigmas typically used 3-4 rotors (chosen from a larger set of available rotors, e.g., 5 or 8) with more complex, notched stepping mechanisms that allowed for more irregular movement.
  • Wirings: EasyEnigma uses randomly generated permutations for rotor and reflector wirings. Historical Enigma rotors and reflectors had specific, carefully designed wirings.
  • Plugboard (Steckerbrett): Most military Enigmas featured a plugboard that swapped pairs of letters before and after the rotor assembly, adding a massive layer of cryptographic strength. EasyEnigma omits this.

In essence, EasyEnigma provides a conceptual taste of rotor machine cryptography without the full operational and cryptographic complexity of its historical counterpart.

Resources

• Wikipedia: Enigma Machine
• CryptoHack - A fun platform to learn modern cryptography by solving challenges.
• Khan Academy: Journey into Cryptography