Calculating the Mean

I thought means were simple. I was wrong.

October 10, 2025

I recently discovered a few surprising things about means:

The arithmetic mean is just one of many types of means. Choosing the right one is crucial.
There’s more than one algorithm for calculating the arithmetic mean. The standard “sum and divide by N” approach isn’t always the ‘best’.

Let’s explore these revelations in more detail.

Which Mean Should We Use? And When?

Data can often be noisy, messy, and hard to interpret. We need tools to summarize it, and a mean is one such tool. It seeks to describe ‘center’ of the data. Of course, the ‘center’ is just one aspect. Other summaries describe how data is spread out (like variance and standard deviation) or the shape of its distribution (skewness and kurtosis).

But what exactly is a mean? And why are there so many? The “right” definition of center depends on the nature of your data and what you want to achieve with your summary.

The Arithmetic Mean (AM)

The arithmetic mean is likely the first type of mean you encountered. It can be calculated by summing all the values and dividing by the count of values:

$\mathcal A(D_n) = \frac{1}{n}\sum_{i=1}^n a_i$ where $D_n = {a_1, a_2, …, a_n}$ is our dataset of $n$ numbers.

One way to understand the arithmetic mean is that it’s the value that minimizes the sum of squared differences between itself and each data point. In this sense, it truly finds a ‘center’ based on minimizing squared Euclidean distances.

Properties of the Arithmetic Mean:

Balance Point: The sum of the deviations of data points from the arithmetic mean is zero ($\sum (a_i - \mathcal A) = 0$). It’s like the fulcrum of a seesaw where the data points are weights.

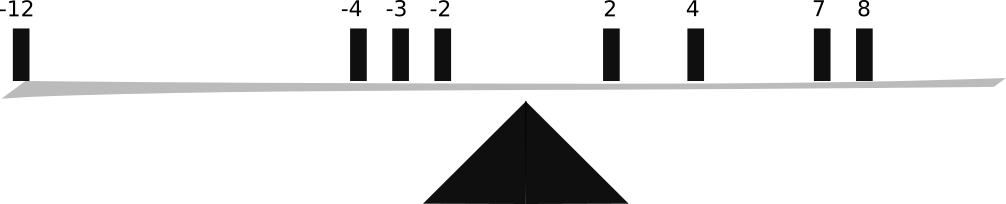
The arithmetic mean acts as a balance point for the data.

Sensitivity to Outliers: The arithmetic mean can be heavily influenced by extreme values (outliers).
Translation Invariance: If you add a constant $c$ to all data points, the mean increases by $c$: $\mathcal A(a_i + c) = \mathcal A(a_i) + c$.
Scale Invariance: If you multiply all data points by a constant $c$, the mean is also multiplied by $c$: $\mathcal A(c \cdot a_i) = c \cdot \mathcal A(a_i)$. ¹

When to use it: The AM is a good general-purpose mean, especially when data is roughly symmetrically distributed (like a Normal distribution) and the sum of the quantities is meaningful.

The Geometric Mean (GM)

The geometric mean provides a different perspective on the ‘center’, especially for quantities that combine multiplicatively. It’s defined as the $n$-th root of the product of $n$ positive numbers:

\[G(D_n) = \bigg(\prod_{i=1}^n a_i \bigg)^{\frac{1}{n}} = \sqrt[n]{a_1 a_2 \cdots a_n}\]

The geometric mean is typically used for positive numbers. If any $a_i=0$, the GM is 0. If negative numbers are involved, the GM can become complex or undefined in real numbers, so its application is generally restricted to positive values. ²

Geometrically, the GM of two numbers, $a$ and $b$, is the side length of a square whose area is equal to the area of a rectangle with sides $a$ and $b$. For three numbers $a, b, c$, it’s the side length of a cube whose volume equals that of a cuboid with sides $a, b, c$. We are summarizing the data by the side length of a hypercube whose volume is the same as the hypercube formed by the data points.

Example: Amplifier Gains Suppose you have 5 amplifiers in series with gains of 2x, 4x, 6x, 9x, and 10x. If you want to replace them with 5 identical amplifiers that achieve the same overall gain, what should the gain of each new amplifier be? The total gain is $2 \times 4 \times 6 \times 9 \times 10 = 4320$x. The arithmetic mean of the gains is $(2+4+6+9+10)/5 = 6.2$x. Using five 6.2x amplifiers would give an overall gain of $(6.2)^5 \approx 91613$x, which is far too high. The correct gain for each replacement amplifier is the geometric mean: $G = (2 \times 4 \times 6 \times 9 \times 10)^{1/5} = (4320)^{1/5} \approx 5.336$x. Five amplifiers with gain 5.336x would give $(5.336)^5 \approx 4320$x.

Properties of the Geometric Mean:

Multiplicative Nature: Suitable for averaging ratios, percentages, growth rates, or other quantities that are multiplicative.
Logarithmic Equivalence: The GM is equivalent to the exponential of the arithmetic mean of the logarithms of the values: $G(D_n) = \exp{\left(\frac {1}{n}\sum_{i=1}^n \ln a_{i}\right)}$ This also means the GM minimizes $\sum (\ln a_i - \ln m)^2$. ³
Effect of Outliers: Less sensitive to very large outliers than the AM, but extremely sensitive to small values (especially values close to zero). A single zero value makes the GM zero.
Scale Invariance: $G(c \cdot a_i) = c \cdot G(a_i)$ for $c > 0$.
Not Translation Invariant.

When to use it: Use the GM for averaging rates of change (e.g., investment returns over several periods), financial ratios, population growth rates, or any scenario where values compound or are products of each other.

Example: The Decathlon

Consider the decathlon, an athletic competition with 10 events. How should we average the scores from these diverse events? Currently, an arithmetic mean (or a sum, which is equivalent for ranking) of points is often used. However, one could argue for the geometric mean.

The geometric mean rewards consistency across all events. A very poor performance (even a score of zero) in one event would severely penalize the overall GM score (a zero score in one event makes the GM zero). This emphasizes all-around ability.

Let’s look at hypothetical scores (normalized for simplicity):

Name	100m	Long Jump	Shot Put	High Jump	400m	110m Hurdles	Discus	Pole Vault	Javelin	1500m	AM	GM (approx)
Bob	8.5	7.5	6.5	8.0	7.0	8.0	6.5	7.0	7.5	7.5	7.40	7.38
Alice	8.0	8.0	7.0	7.5	8.5	7.5	7.0	8.0	8.0	8.0	7.80	7.78
Carl	7.0	2.5	8.0	6.5	6.5	6.5	8.5	6.5	6.0	6.0	6.40	6.00

Alice is consistently good and scores highest on both means. Carl has a very low score in the Long Jump (2.5). His AM is 6.40. His GM is 6.00. The GM penalizes his inconsistent performance more heavily than the AM, relative to the other athletes. If Carl scored 0 in Long Jump, his GM would be 0, while his AM would still be positive (6.15).

The Harmonic Mean (HM)

The harmonic mean is another specialized mean, typically used for averaging rates when the numerator is constant. It’s the reciprocal of the arithmetic mean of the reciprocals of the data points:

$H(D_n) = \frac{n}{\sum_{i=1}^n \frac{1}{a_i}} = \left( \frac{1}{n}\sum_{i=1}^n a_i^{-1} \right)^{-1}$ The HM is also typically used for positive numbers. It’s undefined if any $a_i=0$. It can also be undefined if the sum of reciprocals is zero (which can happen with mixed positive and negative numbers).

Example: Average Speed Suppose you drive a certain distance $D$ at a speed $v_1$, and then drive the same distance $D$ back at a speed $v_2$. What is your average speed for the total trip? It’s not the arithmetic mean $(v_1+v_2)/2$. Total distance = $2D$. Time for first leg = $D/v_1$. Time for second leg = $D/v_2$. Total time = $D/v_1 + D/v_2 = D(1/v_1 + 1/v_2)$. Average speed = Total Distance / Total Time = $2D / (D(1/v_1 + 1/v_2)) = 2 / (1/v_1 + 1/v_2)$. This is the harmonic mean of $v_1$ and $v_2$. For instance, if you go to a destination at 30 km/h and return at 60 km/h, your average speed is $H(30, 60) = 2 / (1/30 + 1/60) = 2 / (3/60) = 120/3 = 40$ km/h. The arithmetic mean would be $(30+60)/2 = 45$ km/h, which is incorrect.

Properties of the Harmonic Mean:

Averaging Rates: Useful for averaging rates (like speed, where distance is constant) or ratios (like P/E ratios in finance, when equally weighted).
Effect of Outliers: Tends to mitigate the impact of large outliers but aggravate the impact of small ones (values close to zero). It gives greater weight to smaller numbers. ⁴
Scale Invariance: $H(c \cdot a_i) = c \cdot H(a_i)$ for $c \neq 0$.
Not Translation Invariant.

When to use it: Use the HM when dealing with rates that have a constant numerator for the quantity being averaged (e.g., km per hour, where km is constant).

Relationship: AM, GM, HM (Pythagorean Means) For any set of positive data points, the following inequality holds: $\mathcal A(D_n) \ge G(D_n) \ge H(D_n)$ Equality holds if and only if all data points $a_i$ are identical. ⁵

Further Reading & Sources:

Wikipedia: Central tendency, Arithmetic mean, Geometric mean, Harmonic mean

Lingering Questions (for the curious):

Variational definitions for GM/HM: As shown, the AM minimizes the sum of squared errors $\sum (a_i - m)^2$. The GM (via its logarithm) minimizes $\sum (\ln a_i - \ln m)^2$. The HM doesn’t have such a simple, direct sum-of-squares variational form but is related to minimizing weighted sums of relative errors in certain contexts.

Alternatives and General Properties of Means

Are there other ways to define a ‘center’? Yes! For example, the Quadratic Mean (Root Mean Square - RMS) is $Q(D_n) = \sqrt{\frac{1}{n}\sum a_i^2}$, used for magnitudes of varying quantities.

More generally, what properties should a “good” mean possess? This depends on the application, but some common desirable properties include:

Permutation Invariance: The order of data points should not matter. (AM, GM, HM satisfy this).
Monotonicity: If we increase some data values (and decrease none), the mean should not decrease. (AM, GM, HM satisfy this).
Dependence on all data: The mean should be a function of all data points. (AM, GM, HM satisfy this).
Scale Invariance: $M(c \cdot a_i) = c \cdot M(a_i)$. AM, GM (for $c>0$), HM (for $c \neq 0$) satisfy this.
Translation Invariance: $M(a_i + c) = M(a_i) + c$. Only the AM among the three Pythagorean means strictly satisfies this. GM and HM do not.
Continuity & Differentiability: The mean should ideally be a continuous and differentiable function of the data (within their valid domains).
Uniqueness: For a given dataset, the mean should be unique.

The choice of mean often boils down to what property you want your ‘center’ to preserve or what kind of ‘error’ you want to minimize.

The ‘Best’ Algorithm for Calculating the Arithmetic Mean

Let’s focus on the arithmetic mean. Calculating it seems trivial: sum the numbers and divide by the count. But what does ‘best’ mean for an algorithm? We could define ‘best’ by:

Reliable Accuracy: How close is the calculated estimate to the true mathematical mean, especially in the face of finite-precision computer arithmetic?
Efficiency: How many computational resources (time, memory) does it take?

The standard algorithm (sum and divide) requires $O(n)$ operations for $n$ data points, which is optimal as you must look at each data point at least once. However, its numerical accuracy can be a concern.

Numerical Stability: The Hidden Pitfall

The “sum and divide” algorithm can suffer from two main numerical issues when implemented on computers with floating-point arithmetic:

Overflow: If you have many large numbers, their sum might exceed the largest representable floating-point number, resulting in infinity.
Loss of Precision (Swamping): When adding a very small number to a very large running sum, the precision of the small number can be lost. Imagine summing $10^{20} + 1 + 1 + \dots + 1$ (many times). If $10^{20}$ is the current sum, adding $1$ might not change the sum at all if the machine’s precision isn’t sufficient. ⁶

More Robust Algorithms: A more numerically stable approach for calculating the mean (and variance) is Welford’s algorithm. It computes the mean incrementally, updating it with each new data point. ⁷

For a sequence $x_1, x_2, \dots, x_n$, the mean $\bar{x}k$ after $k$ points is updated as follows: Initialize $M_1 = x_1$. For $k > 1$, $M_k = M{k-1} + \frac{x_k - M_{k-1}}{k}$. The final mean is $M_n$.

This method is less prone to overflow and catastrophic cancellation (though the latter is more an issue when calculating variance via the two-pass sum-of-squares method). For summing numbers with potentially large differences in magnitude, Kahan summation algorithm can also significantly reduce errors, though Welford’s is often preferred for mean/variance estimation in a streaming context. ⁸

When is the Arithmetic Mean the ‘Optimal’ Estimator?

The sample arithmetic mean is an excellent estimator for the true population mean, especially if the data comes from a Normal (Gaussian) distribution. In fact, it’s the Maximum Likelihood Estimator (MLE) for the mean of a Gaussian. It’s also unbiased and consistent under broad conditions.

However, if the data comes from a distribution with “heavy tails” (i.e., outliers are common), the arithmetic mean can be a poor estimator of the ‘typical’ central value. Its sensitivity to outliers pulls it away from where most of the data might lie.

In such cases, robust estimators of central tendency are preferred:

Median: The middle value of the sorted data. Highly robust to outliers.
Trimmed Mean (or Truncated Mean): Discard a certain percentage of the smallest and largest values, then compute the arithmetic mean of the remaining data.
Winsorized Mean: Instead of discarding outliers, replace them with values at a certain percentile (e.g., replace all values below the 5th percentile with the 5th percentile value, and similarly for the top).
Median of Means: Divide the data into blocks, calculate the median of each block, and then take the mean (or median) of these medians. This can offer good theoretical guarantees for estimating the mean even with heavy-tailed data. ⁹

The choice of estimator depends on assumptions about the underlying data distribution and the goals of the analysis.

Q: What about robust algorithms for calculating the geometric / harmonic mean??

Geometric Mean: Since $G = \exp(\text{AM}(\ln a_i))$, robustness can be improved by robustly calculating the sum of logarithms (e.g., Kahan summation for $\sum \ln a_i$) or by using robust estimators for the mean of $\ln a_i$ (e.g., trimmed mean of $\ln a_i$). Outliers in $a_i$ (very large or very small positive $a_i$) will heavily influence $\ln a_i$.
Harmonic Mean: $H = 1 / \text{AM}(1/a_i)$. It’s very sensitive to $a_i$ values close to zero (as $1/a_i$ becomes huge). Robust versions would need to handle these small values, perhaps by trimming data points whose reciprocals are extreme outliers.

In conclusion, while “calculating the mean” sounds simple, there’s a rich world beneath the surface. Understanding the different types of means, their properties, the nuances of their calculation, and how they relate to the concept of ‘typicality’ is essential for anyone working with data. Choose wisely!

References

Spiegel, M. R. (1992). Theory and Problems of Probability and Statistics (2nd ed.). Schaum’s Outline Series, McGraw-Hill. ↩
“Geometric Mean.” Wolfram MathWorld. https://mathworld.wolfram.com/GeometricMean.html ↩
Bryant, J. (2000). “The Arithmetic, Geometric, and Harmonic Means.” University of Puget Sound. https://www.personal.psu.edu/jxb57/Notes/Means.pdf (Note: This is an example of a typical university resource; actual link may vary or become inactive). A general property discussed in many statistical texts. ↩
“Harmonic Mean.” Wikipedia. https://en.wikipedia.org/wiki/Harmonic_mean ↩
Mitrinović, D. S. (1970). Analytic Inequalities. Springer-Verlag. ↩
Higham, N. J. (2002). Accuracy and Stability of Numerical Algorithms (2nd ed.). SIAM. ↩
Welford, B. P. (1962). “Note on a method for calculating corrected sums of squares and products”. Technometrics, 4(3), 419-420. ↩
Kahan, W. (1965). “Further remarks on reducing truncation errors”. Communications of the ACM, 8(1), 40. ↩
Jerrum, M., Valiant, L., & Vazirani, V. (1986). “Random generation of combinatorial structures from a uniform distribution”. Theoretical Computer Science, 43, 169-188. (Introduced median-of-means for different contexts, but the idea is used in robust estimation). More accessible treatments can be found in robust statistics lecture notes, e.g., by Catoni or Lugosi. ↩