The orderly enumeration of graphs
January 10, 2024
Our goal is to generate all graphs with $n$ nodes. Let’s start with a simple example, generating all graphs with 4 nodes.
However, when generating graphs, we need to be cautious. We need to ensure that none of the generated graphs are the ‘same’. What do we mean by ‘same’?
Consider the four graphs shown below. They all have different edges, but are essentially the same graph: a graph with a 3-chain, and one disconnected node.

Formally, an isomorphism of graphs $G$ and $H$ is a bijection between the vertex sets of $G$ and $H$
\[f\colon V(G)\to V(H)\]such that any two vertices $u$ and $v$ of $G$ are adjacent in $G$ if and only if $f(u)$ and $f(v)$ are adjacent in $H$.
In other words, can we relabel the nodes of one graph to get the other? If so, the graphs are isomorphic.
A naive solution when enumerating graphs is to start with graphs with no edges and add edges one by one. As we go, we check whether the current graph is already in the set of generated graphs (up to isomorphism). If so, discard it, else, add it to the generated set. However, this solution requires checking each graph against all the graphs generated so far. This is expensive!
A cheaper solution is; ordering the graphs and generating the graphs in order (enumeration). By generating the graphs in order, it is not possible to repeat the same graph, see Meringer 2010.
Ordered edges
To order the graphs, we start by ordering the edges.
Each edge can be represented as a tuple of node indices, $(i, j)$. For example, the existence of the edge $(2, 3)$ indicates there is an edge between node 2 and node 3.
Given two edges, $e$, $e’$. We say that $e$ is less than $e’$ if;
\[\begin{aligned} e \le e': i < i' \lor (i = i' \land j < j') \end{aligned}\]This can be visualised as an ordering on a matrix.

Ordered graphs
Now that the edges have an order, we can order graphs. Each graph is ordered by asking; given two graphs, $g, g’$, if we sort their edges (which we can do now that the edges can be ordered) and pair them up. Are the edges in $g$ always less than (or equal) to the edges in $g’$? However, this description is only intuitive.
More formally, for two graphs $g, g’$ we say that $g$ is less than $e’$ if;
\[\begin{aligned} &g < g': \\ (\exists i < \text{min}(t, t')&: e_i < e_i' \land \forall j < i: e_j = e_j') \\ &\lor (t < t' \forall &j \leq t: e_j = e_j') \end{aligned}\]As an example, consider the two graphs below. The first graph is smaller than the second since the edge $(2, 3)$ is smaller than $(2, 4)$.

Canonicity
Now that we have an order on the graphs, we can use this order to define the canonical graph (of a set of isomorphic graphs). The canonical graph is defined to be the minimal graph. The minimal graph is defined to be the smallest graph is the set of all isomorphic graphs.
A graph, $g$ is said to be minimal if, for all permutations in the symmetric group $S_n$, $g$ is the smallest graph.
\[\forall \pi \in S_n : g \leq g_\pi\]It is known that every minimal graph representative with $n$ edges has a minimal subgraph with $n-1$ edges Read 1978. This means that as we construct graphs by adding edges, we only need to pay attention to the minimal graphs, the rest can be ignored as they are not canonical.
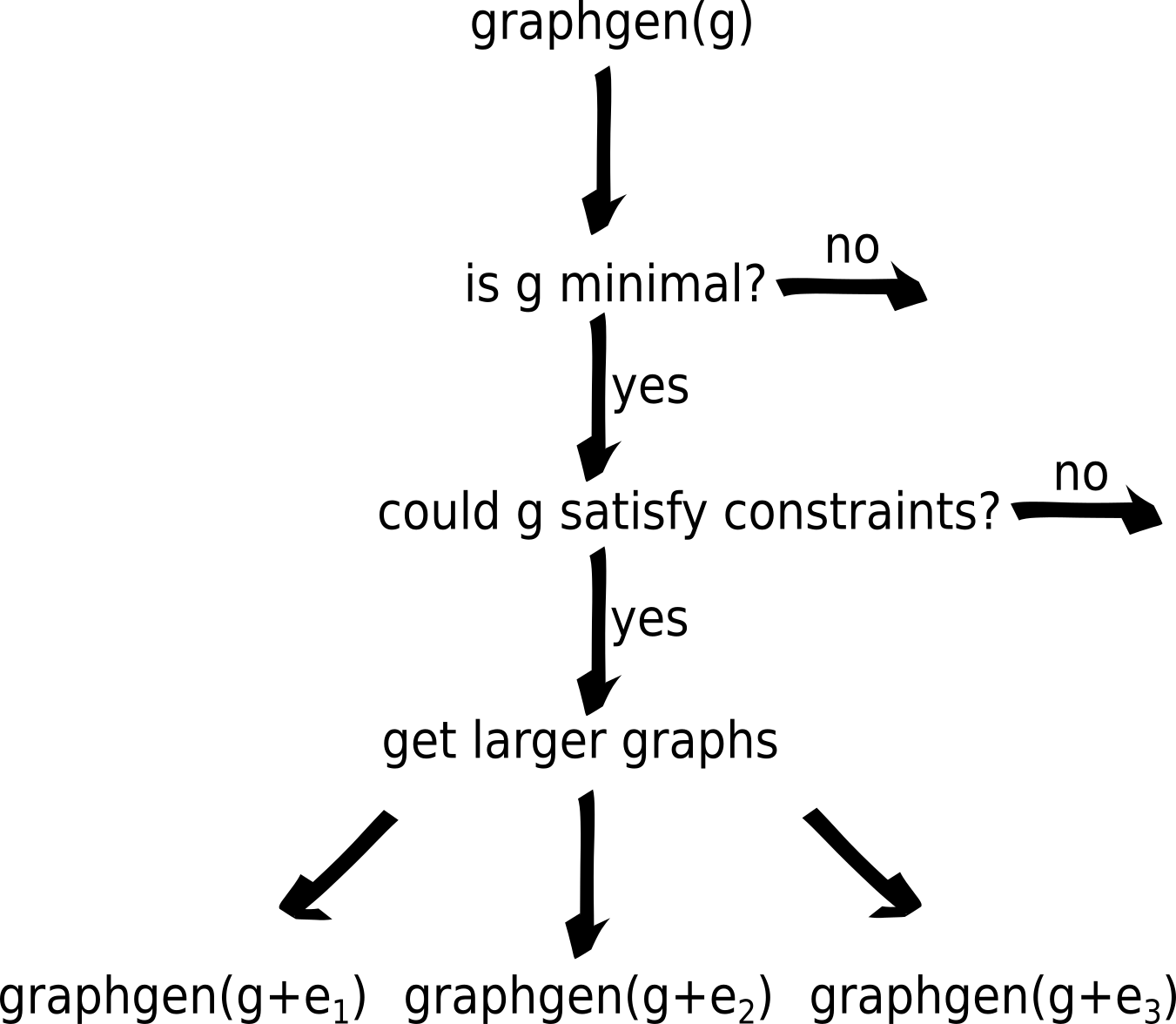
The orderly enumeration algorithm
Now we are ready to describe the orderly enumeration algorithm Meringer 2010. As noted above, we only need to generate minimal graphs, the rest are not canonical. So, we start with the smallest graph, a graph with no edges, and proceed by adding larger edges, in order. As we add edges, we check whether the constructed graph is minimal, if it isn’t, we discard it. This process is visualised below.
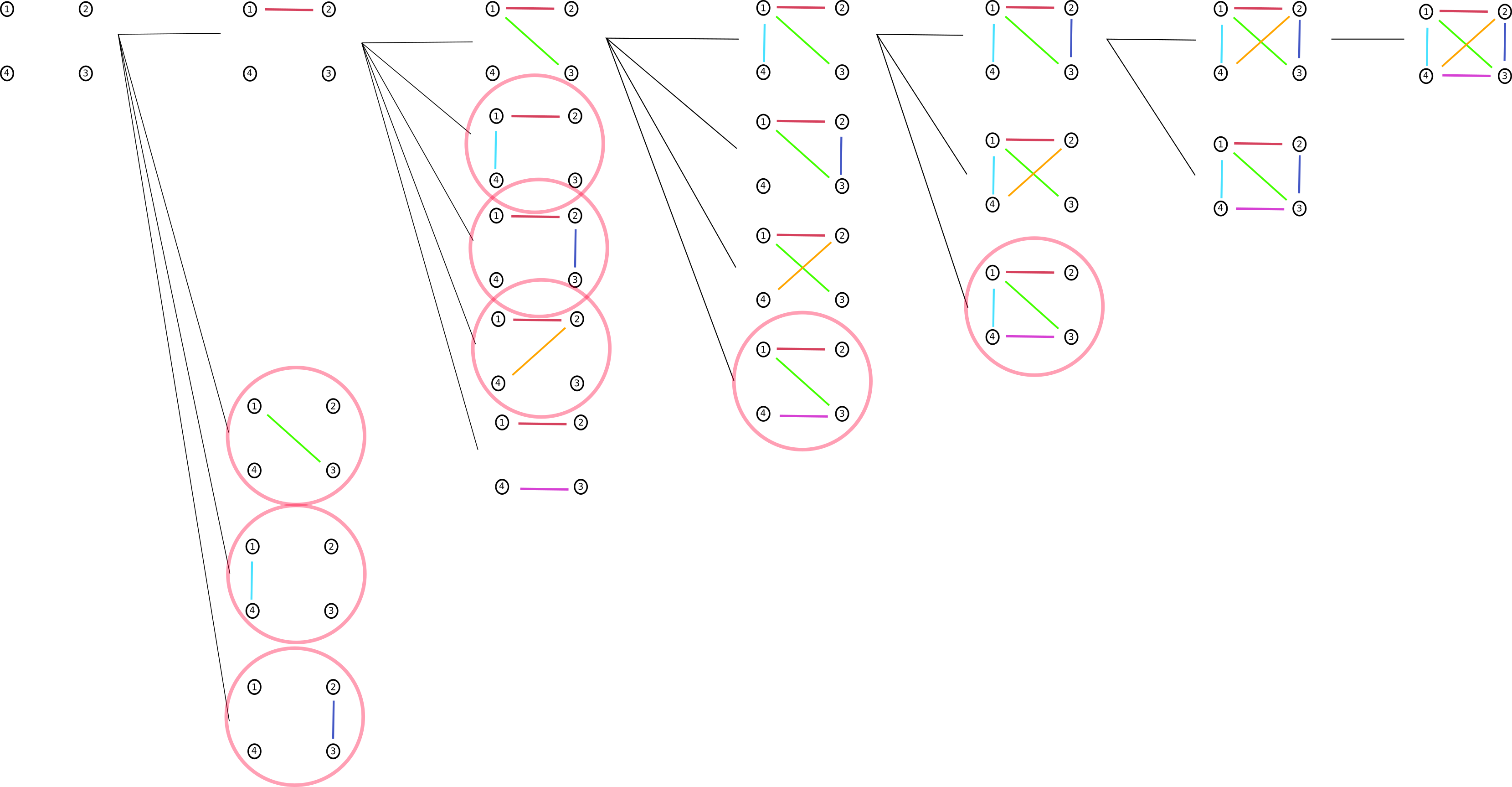
Implementation
I’ve implemented this algorithm in Rust here.