A conservation law for algorithms?
September 26, 2017
What if there was a measure of complexity that was conserved over optimal solutions to the same problem? I am imagining that there is a fundamental complexity to a problem (such as sorting), and the set of optimal solutions lie in a set that conserves the underlying complexity.
Optimal solutions must reflect this complexity if they hope to solve the problem efficiently. But since the complexity is conserved, solutions can trade energy for time for memory useage for latency for parallelism for …
Given a measure of complexity, $\mathcal C$, I want it to satisfy:
Property 1: the complexity of all ‘optimal’ algorithms within the lower bound are equivalent.
Given a problem (such a 3-SAT), one can imagine many different algorithms that may give a solution. Some might be fast, some might be accurate, some might use a lot of memory…
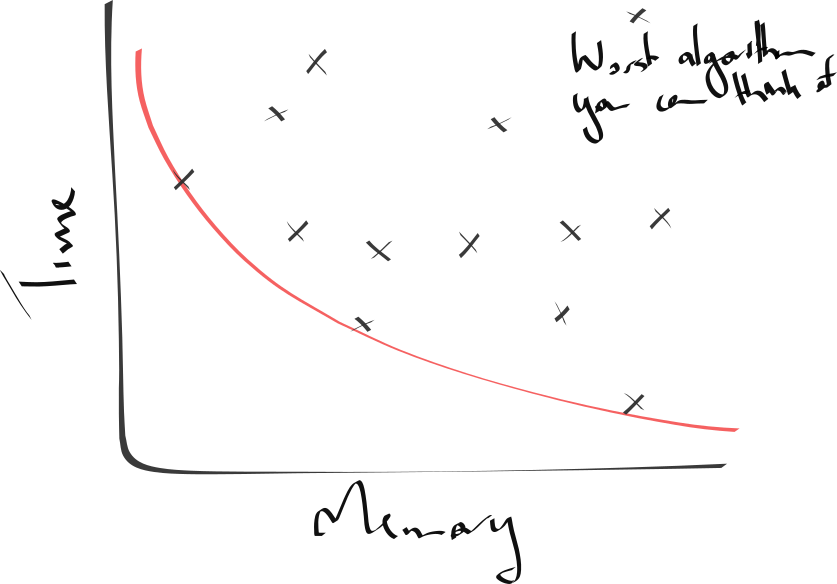
Each of these algorithms must lie on or behind some lower-bound of complexity.
Let $S$ be the set of all solutions in the lower-bound, \(S = \{s : \mathcal C(s) = \mathop{min}_S \mathcal C(s)\}\)
The main intuition behind this equivalence set is that you can trade memory for time, or parallelism for energy, or … but underneath there is still the same fundamental problem you need to solve.
- Can this equivalence set be generalised to approximate algorithms, trading data efficiency for accuracy?
Property 2: The measure of complexity for a problem and an optimal solution is the same.
$s \in S, p \in P, \mathcal C(s) = \mathcal C(p)$.
The intuition is that the problem itself is where the complexity comes from, and is independent of the solution.
- Is it possible to calculate C(p) without considering any solutions?
Property 3: This measure of complexity is proportional to the entropy produced by the implemented algorithm.
The intuition is that algorithms require energy to be run, and this costs us information. More ‘complex’ problems will require more information to be destroyed than others.
Entropy is (/can be viewed as) a measure of the distribution of energy. This measure of complexity should also capture the structure (symmetries, ???) within that energy.
- Could this could give us a lower bound on the information that must be consumed to solve our problem?
- What about the information required to find/construct an element of $P$ or $S$?