Why does poker have many rounds?
December 20, 2024
Imagine that the World series of Poker (with potential winnings of ~\$8 million) only had 1 round. Here we are playing Texas Hold’em, with 8 players.
You have paid the \$1,000,000 entry. You’ve scraped and saved for this moment. You are confident in your ability to read the other players, to bluff, to know when to fold, when to raise.
Here comes your hand; you are dealt 2 clubs and 7 spades (the worst hand possible).


And the flop is 3 clubs, J hearts, 10 clubs. The turn and river are; J spades, 9 hearts.





SHIT.
You lose the hand and are out of the tournament (remember, it’s only 1 round).
The winner, who had the Queen of clubs and the 10 of hearts, takes home \$8 million.
The end.
Many would consider this, 1-round poker, to be an unfair game. It is based, too much, on chance. Whom ever was dealt a good has a BIG advantage.
Instead, poker is played over many rounds. But how many rounds should be played?
The answer to this question depends on the chance we are willing to take that the best player does not win.
How should the game of poker balance luck and skill? Let’s explore this using Kuhn Poker: a stripped-down version where we can mathematically model luck vs skill.
Kuhn poker (3-card poker) is the simplest nontrivial poker game which retains the interesting aspects of texas holdem poker (ie. uncertainty, and bluffing).
- Cards: J, Q, K (ranked low to high)
- Players: 2
- Steps: 1 betting step
Game Flow:
- Each antes 1 unit
- Each gets 1 card (3rd card unused)
- Player 1 acts first: check or bet 1
- If checked, Player 2 can check (showdown) or bet 1
- If bet, Player 2 can fold (P1 wins) or call (showdown)
We can model the game as a decision tree. See below.
By Petr Kadlec - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=48757606
And we can model each players’s strategy as a probability distribution (aka policy) over the possible actions.
Note. We model a player’s strategy as a fixed, mixed policy.
- Fixed: a player’s strategy is fixed before the game starts and does not change during the game, nor between rounds.
- Mixed: a player’s strategy is a probability distribution over the possible actions.
This is a simplification. In reality, a player’s strategy is dynamic and can adapt to the opponent’s strategy.
A player’s strategy is defined by probabilities for each decision. For example we can imagine two different players;
# Returns [prob_check, prob_bet]
def player_a_strategy(card):
# rational strategy
if card == 0: # J
return [0.85, 0.15] # probably check
elif card == 1: # Q
return [0.5, 0.5]
else: # K
return [0.1, 0.9] # probably bet
def player_b_strategy(card):
# random strategy
return [0.5, 0.5] # Mix
Our goal in the following is to calculate the expected win rate for each player. How likely is player A to win a round?
To calculate this, we;
- enumerate all 6 possible card matchups (JvQ, JvK, QvJ, QvK, KvJ, KvQ)
- enumerate all action sequences (check-check, bet-fold, etc.).
- Compute probabilities using each player’s policy.
- accumulate expected values (EV) for each action sequence / card matchup.
def calculate_ev(player1_strat, player2_strat):
cards = [0, 1, 2] # J, Q, K
total_ev = 0
n_combos = 0
for p1_card, p2_card in permutations(cards, 2):
prob_deal = 1 / 6 # 6 possible card matchups
# Get strategies for this hand
p1_act = player1_strat(p1_card)
p2_act = player2_strat(p2_card)
# --- Action Sequence 1: P1 checks -> P2 checks ---
prob = p1_act[0] * p2_act[0] # Both check
if p1_card > p2_card:
payoff = 1 # P1 wins ante
else:
payoff = -1
total_ev += prob_deal * prob * payoff
# --- Action Sequence 2: P1 checks -> P2 bets -> P1 calls ---
prob = p1_act[0] * p2_act[1] * 1.0
if p1_card > p2_card:
payoff = 2 # Pot size 4, net +2
else:
payoff = -2
total_ev += prob_deal * prob * payoff
# --- Action Sequence 3: P1 bets -> P2 calls ---
prob = p1_act[1] * 1.0
if p1_card > p2_card:
payoff = 2
else:
payoff = -2
total_ev += prob_deal * prob * payoff
return (1 + total_ev / 2) / 2 # Convert EV to win probability
With the policies above (rational and random), we can calulate that Player A is 53.1% likely to win a round.
Next, by treating each round as a biased coin flip (53.1% - heads vs. 46.9 - tails), we can calculate the number of rounds needed to be 99% sure Player A wins.
A quick reminder, the probability of getting k heads in n coin flips is given by the binomial distribution:
\[p(k, n) = {n \choose k} p^k (1-p)^{n-k} \\ {n \choose k} = \frac{n!}{k!(n-k)!}\]where ${n \choose k}$ returns the binomial coefficient, $p$ is the probability of heads, and $1-p$ is the probability of tails, $n$ is the number of coin flips, and $k$ is the number of heads.
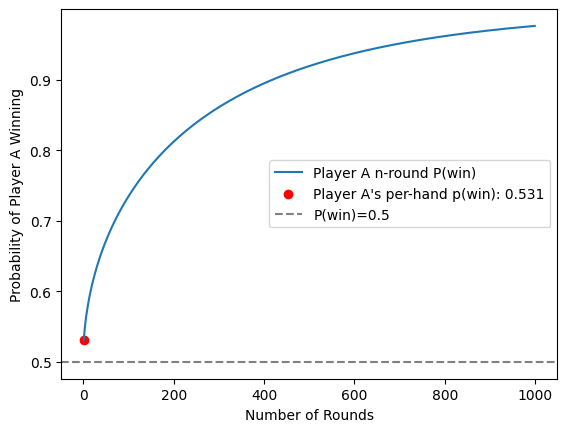
While we know that Player A has a better strategy, it takes many rounds for this to be reflected in the results. With these player strategies, we need 1447 rounds to reach 99% confidence that Player A will win. Or in other words, the probability of player A being ‘unlucky’ and player B being ‘lucky’ is <1%.
Philosophical aside:
How should we deal with the inherent randomness of life?
Life is like poker with only 1 round. You get dealt a hand;
- your genes,
- your parents,
- your socio-economic status,
- a crazy investor,
- cancer.
If it’s a bad hand, tough luck. You lose.
The end.
Earlier, we asked: How many rounds should poker have to balance luck and skill? But the deeper question is: Who gets to decide?
Enter philosopher John Rawls’ veil of ignorance. Imagine designing the rules of poker—or society—without knowing what hand you’ll be dealt. Will you be the pro with a stacked deck or the novice with 2-7 off-suit? Will you inherit wealth or face systemic bias?
Under this veil, rational players wouldn’t tolerate 1-round texas holdem poker. Why? Because a single bad deal could ruin them. Instead, they’d demand:
- Multiple rounds (skill over time)
- Ante redistribution (shared stakes)
- Insurance (protection from ruin)
Sound familiar? These are the same principles behind progressive taxation, public education, and healthcare. The veil forces us to design systems that we’d accept if we might be the unluckiest player.
While many rounds are enough to remove the luck factor from poker, life cannot be played many times. So what would a ‘fair’ game of 1 round poker look like?
In standard poker, luck is hoarded: if you’re dealt a royal flush, you keep all its power. But imagine a variant where, after the river, players must discard one card into a shared “community deck.” Over time, this deck grows, and anyone dealt a historically bad hand (like 2-7 off-suit) can draw from it.
The game stays competitive, but no one’s doomed by a single bad deal. Sound far-fetched? This is how societal redistribution works:
- Progressive taxation is the “discard” phase—those with good hands (wealth, health, privilege) contribute more to the communal stack.
- Social programs act as the redraws—unemployment benefits, public schools, food stamps let people refresh their hands.
- Anti-monopoly laws prevent any player from hoarding all the Kings.
I’m not sure this would be a fun game of poker, but it would be a fairer one.
History is littered with “bad hands” that were once death sentences but are now manageable:
- Polio: Before the 1950s vaccine, polio paralyzed or killed thousands annually. A diagnosis meant life in an iron lung or early death. Today, it’s nearly eradicated. (Vaccines act like a communal redraw—giving everyone a chance to discard the “polio card” from their hand.)
- Childbirth: In 1900, 6–9% of pregnancies ended in maternal death. Modern medicine dropped this to 0.02%.
- Bankruptcy: Before bankruptcy laws, debtors faced prison. Now, legal frameworks let individuals and businesses “fold” without lifelong ruin, preserving their ability to reenter the game.
Poker’s multiple rounds are a concession to luck—a way to ensure skill prevails over time. Life, however, offers no such luxury. We cannot replay our hands, but we can reshape the game itself. By building systems that redistribute luck—through healthcare, education, and social safety nets—we mimic poker’s multi-round fairness in a single-round existence. The question isn’t whether life is fair, but whether we’re going to deal a better deck for those yet to play.