We solve an inverse problem with MAP vs PITS. Here we pick the prior and likelihood to be Gaussian distributions.

\[\begin{align*} p(x) &= \mathcal{N}(0, \sigma_x^2) \\ p(y|x) &= \mathcal{N}(x, \sigma_y^2) \end{align*}\]

Let’s pick the prior to be a Gaussian distribution with mean 0 and standard deviation 1. And the likelihood to be a Gaussian distribution with mean 1 and standard deviation 0.5. We find the MAP solution and the PITS solution.

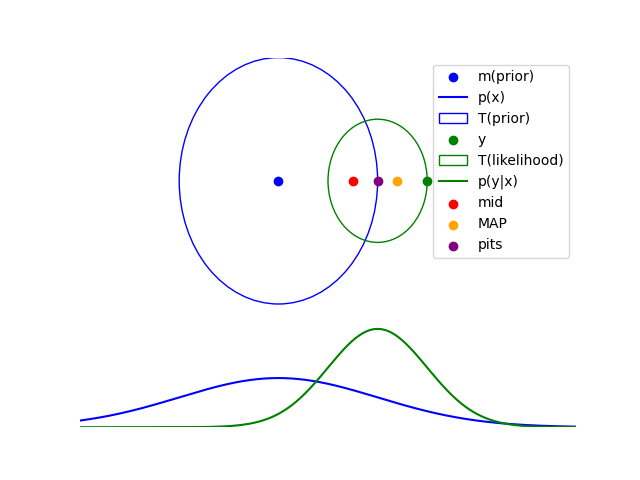
Illustration of the inverse problem for a Gaussian prior and likelihood. Where y is the observation and x is what we want to recover. Top; shows the typical sets of our two distributions and the solutions found by MAP, PITS (where mid is simple the mid point). Bottom; a reminder that we are working with Gaussians.

MAP solution

For Guassian prior and likelihood, can derive the MAP solution in closed form as;

\[\begin{align*} x^*&= \arg \max_x \frac{p(y|x)p(x)}{p(y)} \\ &= \arg \max_x p(y|x)p(x) \\ &= \arg \max_x \log p(y|x) + \log p(x) \\ &= \arg \max_x -\frac{1}{2\sigma_y^2}||y - x||^2 - \frac{1}{2\sigma_x^2}||x||^2 \\ \end{align*}\] \[\begin{align*} \nabla_x \left( -\frac{1}{2\sigma_y^2}||y - x||^2 - \frac{1}{2\sigma_x^2}||x||^2 \right) &= \nabla_x \left( -\frac{1}{2\sigma_y^2}||y - x||^2 \right) + \nabla_x \left( -\frac{1}{2\sigma_x^2}||x||^2 \right) \\ &= \frac{1}{\sigma_y^2}(y - x) - \frac{1}{\sigma_x^2}x \\ &= 0 \\ x^* &= \frac{\sigma_x^2}{\sigma_x^2 + \sigma_y^2}y \\ \end{align*}\]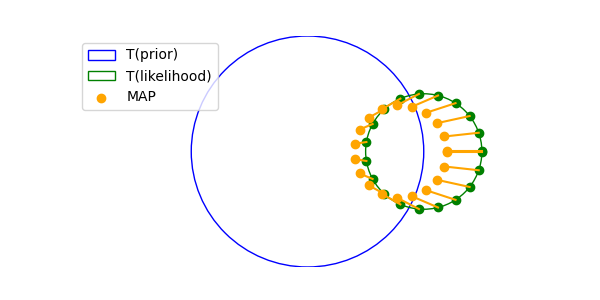

The observed $y$'s are updated to be more likely under the prior.

PITS solution

For Gaussian distributions derived the PITS solution as;

\[\begin{align*} x^* &= \arg \max_{x \in \mathcal T(p(x))_\epsilon} p(y | x) \tag{PITS} \\ &= \arg \max_{x \in \mathcal T(p(x))_\epsilon} \mathcal{N}(x, \sigma_y^2) \\ &= \arg \max_{x \in \mathcal T(p(x))_\epsilon} \exp \left( -\frac{1}{2\sigma_y^2}||y - x||^2 \right) \\ &= \arg \min_{x \in \mathcal T(p(x))_\epsilon} \parallel x - y \parallel^2 \\ \lim_{\epsilon\to 0} \mathcal T(\mathcal N(0, \sigma^2 I))_\epsilon &= \{x ; \parallel x \parallel = \sqrt{d} \sigma \} \\ x^* &= \sqrt{d} \sigma\frac{y}{\parallel y \parallel} \end{align*}\]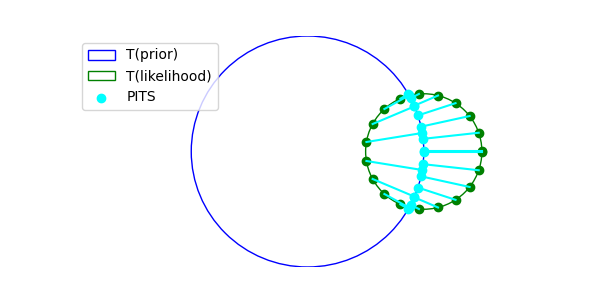

The observed $y$'s are projected into the typical set.

Accuracy

We can compare the accuracy of the MAP and PITS solutions by looking at the mean squared error (MSE) between the true $x$ and the estimated $x$.

\[\text{err} = \frac{1}{N \sqrt{d}} \sum_{i=1}^N ||x_i - x_i^*||^2 \\\]

We find that MAP provides slightly more accurate solutions than PITS. For example, if we pick d=2048, average over 10000 samples. We get an average normalised error of MAP $0.45$ and PITS $0.46$.