What can I gain if, rather than planning into the future, I can plan backwards from my goals (or both)?
(I imagine these ideas are well known within the planning/AI, automated-proving, graph and tree-search communities. But I just needed to get these ideas out of my head.)
Sepcifically, I am interested in; what problems can we solve more efficiently if we (also) have access to an inverse model of the dynamics of a system. This question was inspired by a link I can no longer find (argh!).
The general gist of the idea is that: Supposedly people tend to be bad at planning forward in time. For example, I might want to stop climate change, and I happen to be a writer. Therefore I start writing about climate change. But, there is no reason that writing will lead to a stop of climate change, it is just what I am able to do. Instead you could plan backwards from your goal. Stop climate change. Ok, how can I stop the release CO2 into the atmosphere. Who/what releases CO2? Cars. How can I convince them to stop releasing CO2?
Ok. Let the state of a system be $s_t$ and how it changes over time be described by the transition function, $s_{t+1} = \tau(s_t)$. Typical approaches to planning (at least in reinforcement learning) involve using the transition function to simulate future events.
Let’s consider the U-problem. Imagine the goal is to get from $A$ to $B$ (left). Additionally, the learner has been given a shaped reward, $r$, encouraging smaller distances between the agent ‘s position, $p$ and $B$. $r_t = -\parallel p_t - \mathcal B \parallel + 1_{p=\mathcal B}$.
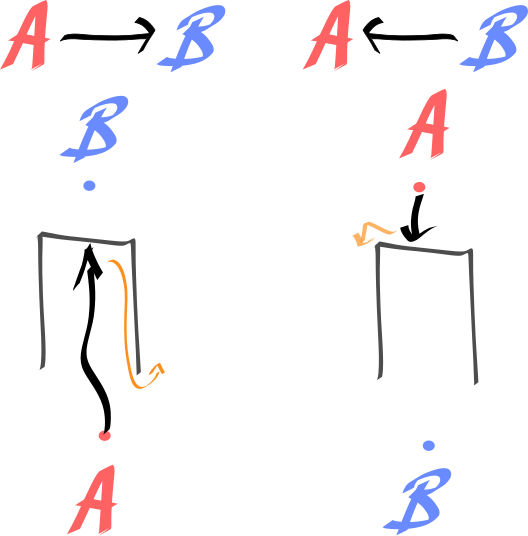
This shaped reward makes learning impossible for many well known reinforcment learning algorithms (Q, PG, …) without the intelligent use of exploration! The agent will quickly get stuck in the U, optimising the olny rewards they have ever and will ever see. Similarly, planning based approaches would fall into a similar trap, when guided by the shaped reward. They would first search trajectories that went straight into the cup.
As shown in the picture on the right, suddenly the problem becomes a lot easier when inverted. Sure, the shaped reward will lead he agent to get stuck on the horizontal surface of the cup, but the chance of discovering extra progress by going left or right is much more likely than discovering a way out of the cup.
Deduction + Abduction
Imagine you are an agent in a 2d environment. But, rather than having access to the usual euclidean metric to guide you, you have nothing. This is a common situation in the RL setting. The learner does not know how its actions move it around the space it is in, and it does not know which actions will lead to a reward.
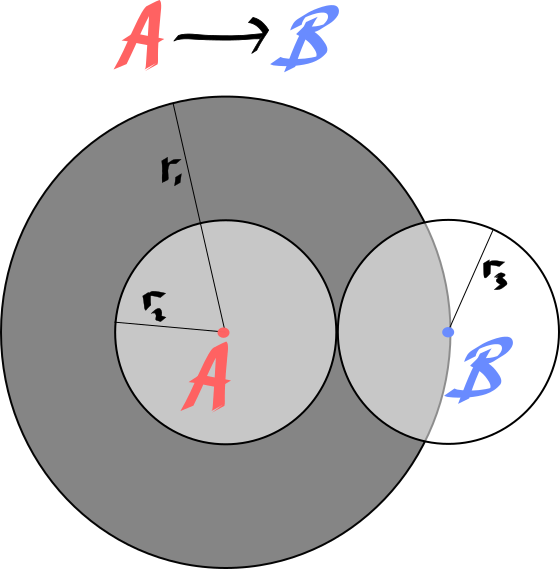
(we know $r_1 = r_2 + r_3$)
So, how much smaller is the search space when we plan from $A$ and $B$?
- Planning from A xor B: $\pi r_1^2$
- Planning from A and B: $\pi r_2^2 + \pi r_3^2$
Reduction in search space
\[\begin{align} &= \pi (r_2 + r_3)^2 - (\pi r^2_2 + \pi r_3^2)\\ &= 2r_2r_3\\ \\ \Delta &= Vol(r_1) - Vol(r_2) - Vol(r_3)\\ &= \mathcal O(r^{d-1}) \\ \end{align}\]Or, maybe this is clearer in the descrete setting, where were are doing a tree search over possibilities. In the naive case, planning from $A$, or $B$, there are $2^6$ states that are searched. While if we search from $A$ and $B$ search there are $2\times 2^3=2^4$ states searched.
Questions/thoughts
- If you have many subgoals along the way we might be able to achieve $\mathcal O(\frac{r}{n}^{d-1})$, where $n$ is the number of subgoals. But this assumes that the subgoals are acutally helpful and along the optimal path. If not this could lead to far worse performance.
- This ideas simply requires symmetry. All we are doing is exploiting the symmetry that the path from A to B is the same as the path from B to A. (Q: when is this not the case?)
- But! We have introduced another computation (which I didn’t notice initially). Now we must compare the leaves in each search tree to check if the two searches have intersected. (this could be quite expensive???)